[Chapter Sixteen][Previous]
[Next] [Art of
Assembly][Randall Hyde]
Art of Assembly: Chapter Sixteen
- 16.6 - Semantic Rules and Actions
- 16.7 - Constructing Patterns for the
MATCH Routine
16.6 Semantic Rules and Actions
Automata theory is mainly concerned with whether or not a string matches
a given pattern. Like many theoretical sciences, practitioners of automata
theory are only concerned if something is possible, the practical applications
are not as important. For real programs, however, we would like to perform
certain operations if we match a string or perform one from a set of operations
depending on how we match the string.
A semantic rule or semantic action is an operation you perform based upon
the type of pattern you match. This is, it is the piece of code you execute
when you are satisfied with some pattern matching behavior. For example,
the call to patgrab in the previous section is an example of
a semantic action.
Normally, you execute the code associated with a semantic rule after returning
from the call to match. Certainly when processing regular expressions,
there is no need to process a semantic action in the middle of pattern matching
operation. However, this isn't the case for a context free grammar. Context
free grammars often involve recursion or may use the same pattern several
times when matching a single string (that is, you may reference the same
nonterminal several times while matching the pattern). The pattern matching
data structure only maintains pointers (EndPattern, StartPattern,
and StrSeg) to the last substring matched by a given pattern.
Therefore, if you reuse a subpattern while matching a string and you need
to execute a semantic rule associated with that subpattern, you will need
to execute that semantic rule in the middle of the pattern matching operation,
before you reference that subpattern again.
It turns out to be very easy to insert semantic rules in the middle of a
pattern matching operation. All you need to do is write a pattern matching
function that always succeeds (i.e., it returns with the carry flag clear).
Within the body of your pattern matching routine you can choose to ignore
the string the matching code is testing and perform any other actions you
desire.
Your semantic action routine, on return, must set the carry flag and it
must copy the original contents of di into ax.
It must preserve all other registers. Your semantic action must not call
the match routine (call sl_match2 instead). Match
does not allow recursion (it is not reentrant) and calling match
within a semantic action routine will mess up the pattern match in progress.
The following example provides several examples of semantic action routines
within a program. This program converts arithmetic expressions in infix
(algebraic) form to reverse polish notation (RPN) form.
; INFIX.ASM
;
; A simple program which demonstrates the pattern matching routines in the
; UCR library. This program accepts an arithmetic expression on the command
; line (no interleaving spaces in the expression is allowed, that is, there
; must be only one command line parameter) and converts it from infix notation
; to postfix (rpn) notation.
.xlist
include stdlib.a
includelib stdlib.lib
matchfuncs
.list
dseg segment para public 'data'
; Grammar for simple infix -> postfix translation operation
; (the semantic actions are enclosed in braces}:
;
; E -> FE'
; E' -> +F {output '+'} E' | -F {output '-'} E' | <empty string>
; F -> TF'
; F -> *T {output '*'} F' | /T {output '/'} F' | <empty string>
; T -> -T {output 'neg'} | S
; S -> <constant> {output constant} | (E)
;
; UCR Standard Library Pattern which handles the grammar above:
; An expression consists of an "E" item followed by the end of the string:
infix2rpn pattern {sl_Match2,E,,EndOfString}
EndOfString pattern {EOS}
; An "E" item consists of an "F" item optionally followed by "+" or "-"
; and another "E" item:
E pattern {sl_Match2, F,,Eprime}
Eprime pattern {MatchChar, '+', Eprime2, epf}
epf pattern {sl_Match2, F,,epPlus}
epPlus pattern {OutputPlus,,,Eprime} ;Semantic rule
Eprime2 pattern {MatchChar, '-', Succeed, emf}
emf pattern {sl_Match2, F,,epMinus}
epMinus pattern {OutputMinus,,,Eprime} ;Semantic rule
; An "F" item consists of a "T" item optionally followed by "*" or "/"
; followed by another "T" item:
F pattern {sl_Match2, T,,Fprime}
Fprime pattern {MatchChar, '*', Fprime2, fmf}
fmf pattern {sl_Match2, T, 0, pMul}
pMul pattern {OutputMul,,,Fprime} ;Semantic rule
Fprime2 pattern {MatchChar, '/', Succeed, fdf}
fdf pattern {sl_Match2, T, 0, pDiv}
pDiv pattern {OutputDiv, 0, 0,Fprime} ;Semantic rule
; T item consists of an "S" item or a "-" followed by another "T" item:
T pattern {MatchChar, '-', S, TT}
TT pattern {sl_Match2, T, 0,tpn}
tpn pattern {OutputNeg} ;Semantic rule
; An "S" item is either a string of one or more digits or "(" followed by
; and "E" item followed by ")":
Const pattern {sl_Match2, DoDigits, 0, spd}
spd pattern {OutputDigits} ;Semantic rule
DoDigits pattern {Anycset, Digits, 0, SpanDigits}
SpanDigits pattern {Spancset, Digits}
S pattern {MatchChar, '(', Const, IntE}
IntE pattern {sl_Match2, E, 0, CloseParen}
CloseParen pattern {MatchChar, ')'}
Succeed pattern {DoSucceed}
include stdsets.a
dseg ends
cseg segment para public 'code'
assume cs:cseg, ds:dseg
; DoSucceed matches the empty string. In other words, it matches anything
; and always returns success without eating any characters from the input
; string.
DoSucceed proc far
mov ax, di
stc
ret
DoSucceed endp
; OutputPlus is a semantic rule which outputs the "+" operator after the
; parser sees a valid addition operator in the infix string.
OutputPlus proc far
print
byte " +",0
mov ax, di ;Required by sl_Match
stc
ret
OutputPlus endp
; OutputMinus is a semantic rule which outputs the "-" operator after the
; parser sees a valid subtraction operator in the infix string.
OutputMinus proc far
print
byte " -",0
mov ax, di ;Required by sl_Match
stc
ret
OutputMinus endp
; OutputMul is a semantic rule which outputs the "*" operator after the
; parser sees a valid multiplication operator in the infix string.
OutputMul proc far
print
byte " *",0
mov ax, di ;Required by sl_Match
stc
ret
OutputMul endp
; OutputDiv is a semantic rule which outputs the "/" operator after the
; parser sees a valid division operator in the infix string.
OutputDiv proc far
print
byte " /",0
mov ax, di ;Required by sl_Match
stc
ret
OutputDiv endp
; OutputNeg is a semantic rule which outputs the unary "-" operator after the
; parser sees a valid negation operator in the infix string.
OutputNeg proc far
print
byte " neg",0
mov ax, di ;Required by sl_Match
stc
ret
OutputNeg endp
; OutputDigits outputs the numeric value when it encounters a legal integer
; value in the input string.
OutputDigits proc far
push es
push di
mov al, ' '
putc
lesi const
patgrab
puts
free
stc
pop di
mov ax, di
pop es
ret
OutputDigits endp
; Okay, here's the main program which fetches the command line parameter
; and parses it.
Main proc
mov ax, dseg
mov ds, ax
mov es, ax
meminit ; memory to the heap.
print
byte "Enter an arithmetic expression: ",0
getsm
print
byte "Expression in postfix form: ",0
ldxi infix2rpn
xor cx, cx
match
jc Succeeded
print
byte "Syntax error",0
Succeeded: putcr
Quit: ExitPgm
Main endp
cseg ends
; Allocate a reasonable amount of space for the stack (8k).
sseg segment para stack 'stack'
stk db 1024 dup ("stack ")
sseg ends
; zzzzzzseg must be the last segment that gets loaded into memory!
zzzzzzseg segment para public 'zzzzzz'
LastBytes db 16 dup (?)
zzzzzzseg ends
end Main
16.7 Constructing Patterns for the MATCH Routine
A major issue we have yet to discuss is how to convert regular expressions
and context free grammars into patterns suitable for the UCR Standard Library
pattern matching routines. Most of the examples appearing up to this point
have used an ad hoc translation scheme; now it is time to provide an algorithm
to accomplish this.
The following algorithm converts a context free grammar to a UCR Standard
Library pattern data structure. If you want to convert a regular expression
to a pattern, first convert the regular expression to a context free grammar.
Of course, it is easy to convert many regular expression forms directly
to a pattern, when such conversions are obvious you can bypass the following
algorithm; for example, it should be obvious that you can use spancset
to match a regular expression like [0-9]*.
The first step you must always take is to eliminate left recursion from
the grammar. You will generate an infinite loop (and crash the machine)
if you attempt to code a grammar containing left recursion into a pattern
data structure. You might also want to left factor the grammar while you
are eliminating left recursion. The Standard Library routines fully support
backtracking, so left factoring is not strictly necessary, however, the
matching routine will execute faster if it does not need to backtrack.
If a grammar production takes the form A  B C
where A, B, and C are nonterminal symbols, you
would create the following pattern:
B C
where A, B, and C are nonterminal symbols, you
would create the following pattern:
A pattern {sl_match2,B,0,C}
This pattern description for A checks for an occurrence of a B pattern followed
by a C pattern.
If B is a relatively simple production (that is, you can convert it to a
single pattern data structure), you can optimize this to:
A pattern {B's Matching Function, B's parameter, 0, C}
The remaining examples will always call sl_match2, just to
be consistent. However, as long as the nonterminals you invoke are simple,
you can fold them into A''s pattern.
If a grammar production takes the form A  B | C
where A, B, and C are nonterminal symbols, you
would create the following pattern:
B | C
where A, B, and C are nonterminal symbols, you
would create the following pattern:
A pattern {sl_match2, B, C}
This pattern tries to match B. If it succeeds, A succeeds; if it fails,
it tries to match C. At this point, A''s success or failure is the success
or failure of C.
Handling terminal symbols is the next thing to consider. These are quite
easy - all you need to do is use the appropriate matching function provided
by the Standard Library, e.g., matchstr or matchchar.
For example, if you have a production of the form A  abc | y you would
convert this to the following pattern:
abc | y you would
convert this to the following pattern:
A pattern {matchstr,abc,ypat}
abc byte "abc",0
ypat pattern {matchchar,'y'}
The only remaining detail to consider is the empty string. If you have a
production of the form A 
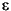 then you need to
write a pattern matching function that always succeed. The elegant way to
do this is to write a custom pattern matching function. This function is
then you need to
write a pattern matching function that always succeed. The elegant way to
do this is to write a custom pattern matching function. This function is
succeed proc far
mov ax, di ;Required by sl_match
stc ;Always succeed.
ret
succeed endp
Another, sneaky, way to force success is to use matchstr and
pass it the empty string to match, e.g.,
success pattern {matchstr, emptystr}
emptystr byte 0
The empty string always matches the input string, no matter what the input
string contains.
If you have a production with several alternatives and 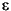 is one of them,
you must process
is one of them,
you must process 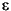 last. For example, if you have the productions A
last. For example, if you have the productions A
 abc | y | BC |
abc | y | BC |
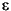 you would use the following
pattern:
you would use the following
pattern:
A pattern {matchstr,abc, tryY}
abc byte "abc",0
tryY pattern {matchchar, 'y', tryBC}
tryBC pattern {sl_match2, B, DoSuccess, C}
DoSuccess pattern {succeed}
While the technique described above will let you convert any CFG to a pattern
that the Standard Library can process, it certainly does not take advantage
of the Standard Library facilities, nor will it produce particularly efficient
patterns. For example, consider the production:
Digits  0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Converting this to a pattern using the techniques described above will yield
the pattern:
Digits pattern {matchchar, '0', try1}
try1 pattern {matchchar, '1', try2}
try2 pattern {matchchar, '2', try3}
try3 pattern {matchchar, '3', try4}
try4 pattern {matchchar, '4', try5}
try5 pattern {matchchar, '5', try6}
try6 pattern {matchchar, '6', try7}
try7 pattern {matchchar, '7', try8}
try8 pattern {matchchar, '8', try9}
try9 pattern {matchchar, '9'}
Obviously this isn't a very good solution because we can match this same
pattern with the single statement:
Digits pattern {anycset, digits}
If your pattern is easy to specify using a regular expression, you should
try to encode it using the built-in pattern matching functions and fall
back on the above algorithm once you've handled the low level patterns as
best you can. With experience, you will be able to choose an appropriate
balance between the algorithm in this section and ad hoc methods you develop
on your own.
- 16.6 - Semantic Rules and Actions
- 16.7 - Constructing Patterns for the
MATCH Routine
Art of Assembly: Chapter Sixteen - 29 SEP 1996
[Chapter Sixteen][Previous]
[Next] [Art of
Assembly][Randall Hyde]
 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
 B C
where A, B, and C are nonterminal symbols, you
would create the following pattern:
B C
where A, B, and C are nonterminal symbols, you
would create the following pattern:  B | C
where A, B, and C are nonterminal symbols, you
would create the following pattern:
B | C
where A, B, and C are nonterminal symbols, you
would create the following pattern:  abc | y you would
convert this to the following pattern:
abc | y you would
convert this to the following pattern: 
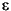 then you need to
write a pattern matching function that always succeed. The elegant way to
do this is to write a custom pattern matching function. This function is
then you need to
write a pattern matching function that always succeed. The elegant way to
do this is to write a custom pattern matching function. This function is
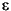 is one of them,
you must process
is one of them,
you must process 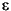 last. For example, if you have the productions A
last. For example, if you have the productions A
 abc | y | BC |
abc | y | BC |
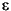 you would use the following
pattern:
you would use the following
pattern: 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9